許多產品是第一次開發,開天闢地以來沒有人知道要如何訂定參數規格。設計者對於這樣的狀況往往會陷於一種焦慮,並且胡亂訂出一個數值作為暫定規格,然而這樣的暫定數值註定無法反應產品實現過程的諸多變異,進而在下一次生產時倉促修改規格。
不斷的修修改改就好像衣物的補丁一樣讓整件產品充滿了破洞,就算這件衣服還能穿也早已不能見人了。
另一方面,台灣許多公司都會讓工程師學習各種品質工具,像SPC就是大家耳熟能詳的一種。但當我們遇到上述定義規格的困擾時,卻往往不知道SPC原來可以協助我們找出暫定的規格。
這篇文章就指點你如何在產品實現的過程中可以使用SPC加以訂定產品參數的規格。
- 將你感興趣的參數丟到製程裡面 樣本數須 > 100
- 撈取製程所產生的參數
- 將參數繪製成管制圖 例如X-bar R Chart or X-bar S Chart
- 觀察數據是否呈現常態分佈
- 觀察數據是否呈現統計穩定(落在管制界線內 & 沒有特殊patterns)
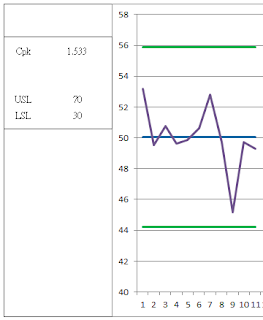
若上述的流程都完全符合,也就是說你的參數目前呈現統計穩定的狀態,我們就可以運用Cpk > = 1.33的算式帶入未知數USL & LSL加以計算。
Cpk = min{ (USL-Xbarbar)/(3*R-bar/d2), (Xbarbar-LSL)/(3*R-bar/d2)} >= 1.33,帶入X-barbar、R-bar及d2,我們就能計算出USL和LSL。
這種算法適用於雙邊規格的計算。
實務範例
最近公司要加一個測項做為新的監控項目,剛好便拿來做為示範。首先我們先將原始資料依照時間順序排序再繪製成管制圖。
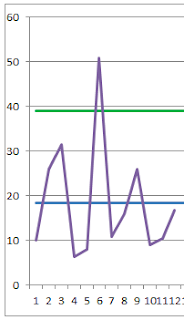
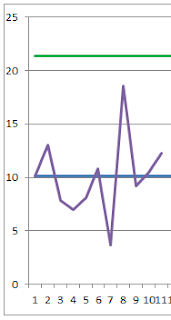
這裡我們選用n=5的X-bar R管制圖,得到了12組數據(12*5 = 60機台數值) 如圖一。雖然比期望的100台數據來得少,但這已經是我們現有能夠得到的數據了,而管制圖的R Chart顯示全距的變異超出管制界限。
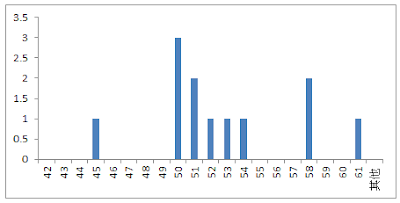
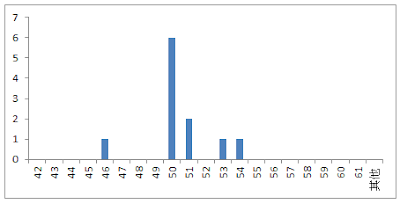
這時候我們回去翻查原始資料,發現有四筆資料確實比較異常,並且由於RD的分析,我們已經知道該異常均屬於同一原因並排除。所以我們回頭將刪除後的數據再繪製成管制圖,發現此時X-bar & R Chart均已在統計穩定狀態。將X-bar數據畫成直方圖也觀察到數據滿像常態分配,因此我們不能拒絕此為常態分配的假設。