損失函數、田口博士與戴明博士
損失函數是品質工程發展中的一項極重要的觀念,最早是由田口博士(Genichi Taguchi)所提出,目的是協助工業界更好地掌握變異所帶來的品質成本問題,這些成本在短期內或許微不足道,但卻會累積成龐大的社會成本。由於產品偏移了客戶需求(Target),這中間會有更多零件的磨損、難以組裝的問題、較低的產品可靠度等等。
但是損失函數Loss Function的概念令人匪夷所思,品質的損失不是來自於不合格品嗎?合規的產品何來損失之有?產品要嘛合格要嘛不合格,損失函數的概念根本多此一舉。
上述的觀念仍然廣泛出現在現今的製造業,多數人仍採用傳統的「符合規格」觀念,而缺乏「損失函數」的概念,這中間的差異到底在哪裡?戴明博士早就指出真正的原因出在大家沒有「變異知識」的觀念。變異知識Variation Knowledge指的是清楚認知到沒有兩個一樣的事物,事務彼此之間沒有一不一樣的問題,只有不一樣的程度問題。只有清楚了解變異知識並理解它的存在,我們才能進一步學習損失函數的概念。
評估損失的方法
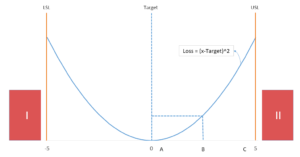
損失函數考量實際製造值與目標值Target的差異,並將此差異作為評估損失的重要指標,讓距離目標值越遠的製造值擁有較多的「損失」,表示我們造成的損失越多。實際製造值與目標值的差異就是變異,當變異越大則損失越多,則我們可以寫成等式:L = (x-target)^2。
假想我們今天生產了三個相同零件ABC,其製造規格為0 +/- 5,意即此產品在[-5, 5]都算合規;目前這三個零件均合規,且品質特性分別為:0、2.5、5,如上圖所示。以傳統的「符合規格」觀念,這三個零件沒有差異,同樣都是合規判定允收,成本是0。但若以損失函數的觀念進行評估則可以發現,這三者的損失函數分別為:(0-0)^2=0、(2.5-0)^2=6.25、(5-0)^2=25,整體的成本是Σ Li = 0 + 6.25 + 25 = 31.25。我們的目的是最小化損失函數,這需要妥善的前期規劃、嚴謹的製程控制及長期的可靠度提升方案才有機會完成。
事實上我們當然不可能只製造3個零件,在3個零件背後往往是數以千萬計的生產數量,此時若此生產條件的製程能力大部分落在C點,則造成的損失還真的不是普通的大。損失函數之所以使用二次方程表達的原因很單純,它想凸顯一件事:距離Target越遠的實際值須擁有更多的損失。
損失函數帶來的優點
- 了解變異知識對提升產品品質、強化企業利潤、降低社會成本的用處
- 有助於說服企業拋棄舊有的「符合規格」觀念。
- 倡導「品質就是降低變異」的觀念,並且量化變異所帶來的額外損失。
瀏覽次數: -
請問Jeff,如果是最大製程損失您會怎麼定義,在數學上或是文字定義上,謝謝您!!
Hi Kevin,
L = (x-target)^2涵式的極值出現在規格的兩側, 偏越遠則損失越大。
這兩者不一樣。
區間估計是在說透過抽樣樣本的樣本值去推估母體參數的位置;
而損失函數是在表達產品變異的概念, 並且結合成本的觀念, 拋棄了傳統的合規格的品質觀點。
損失函數我第一次聽到,受益良多。而我知道推論統計裡,有一個是講在一批(不管有限群體或無限群體)視為常態分配(Z分配)(或非常態分配(t分配))的母批中,取樣本得平均值以及樣本標準差,推論在95%信賴區間內,推論有多不合格的機率,再推論出多少不合格品。依我淺見,這兩者都是一樣的道理。請教,我這樣想法,是正確嗎?