【品質工程】品質管理的數學工具_統計分配

大家學統計許多分配時都很痛苦，絕大多數是因為不知道學這些分配要做什麼用。其實要解決工作上的疑難雜症，很多時候要請出統計分配出來，這篇文章就簡單介紹一些分配。

大家又要問這些分配能有什麼實用性呢？發明出這些模型到底要幹嘛？其實大家就把統計的式子想成是形容群體或者形容事件的描述就行了；這些函式往往藉由參數的設定以及公式的推導，就能完整形容群體及事件的分布狀態。這些分配不僅很美觀，也帶來許多便利，我們以下就一一列舉：

常態分配Normal Distribution

平均值正負1個標準差曲面下面積 = 0.6826
平均值正負2個標準差曲面下面積 = 0.9544
平均值正負3個標準差曲面下面積 = 0.9974

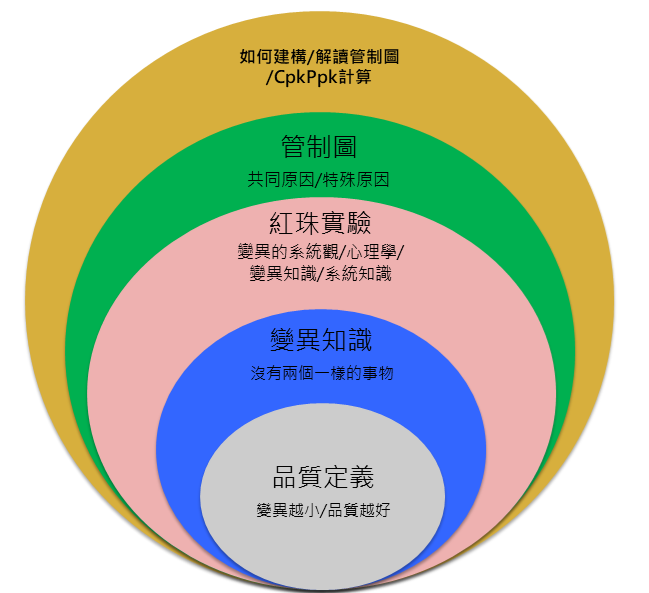
常態分配的特性在品質工程裡面被拿來作為管制圖的建構原理，我們熟知的管制圖3倍sigma上下限就是從常態分配中推演得來。

二項分配 Binomial Distribution

某事件可區分為「成功」或「失敗」兩種結果，而且我們想要知道在第n次出現成功i次的機率。值得注意的是，每次事件彼此都是獨立的關係。這樣的事件就可被稱為二項分配，參數是：試驗n次，以及成功的機率P。

p(i) = (ni)*(p^n)*(q^(n-i)) , i=1,2,3…n 其中 q = 1-p 代表失敗的機率

期望值E(X) = np 變異數Var(X) = npq 這個性質很好證明，大家有興趣可以證一下。
例如躑一硬幣10次，想知道正面朝上的次數為4次的機率，
f(4; 10, 0.5) = (10/4)*(0.5^4)*(0.5^6) = 0.205 = 20.5%

幾何分配 Geometric Distribution

Poisson分配

機率密度函數是 參數是lambda意義為到達率。期望值E(X) = lambda 變異數Var(X) = lambda，如果我們要監控不合格點數的話 我們就可以使用Poisson分配。不合格點數管制圖就是運用Poisson分配所得到的管制圖

學習統計分配的意義

學習事件、樣本空間、機率以及統計對很多人來說都是很痛苦的事情，我以前讀書的時候也常感困惑，老師經常沒有說明這些東西有什麼明確的用途。但現今品質工程領域其實就是應用這些統計相關知識在運作的，只是業界往往不重視。

第一 大家當初讀書時就沒有讀懂，出社會後自然更不想理解
第二 不想理解知識之後，反過來就會評論這知識沒有實用價值
第三 知識沒有實用價值是因為我懂比較多實務經驗，實務經驗比你的知識有價值多了

從事品質改善的專家都知道，我們業界運用知識的機會太少了，以至於許多問題反覆發生，而其實早有解答。學習統計分配的意義在於我們透過細心確認問題是否符合分配的特性，然後利用分配的性質建構出管理工具，再透過管理工具進行事前的預防、管理工作，讓知識成為我們工作流程的一部分，並且透過職場中的統計教育訓練，讓使用者(這裡泛指作業員或工程師)、管理者(這裡泛指經理等主管)都能熟悉這些工具，使其不要誤用統計工具、正確認知統計知識的價值 我們才能得到真正好的品質。

相關文章

【品質工程】品質管理的數學工具_貝氏定理Bayesian Theorem
【品質工程】品質管理的數學工具_ANOVA變異數分析
【品質工程】品質管理的數學工具_假設檢定