漏斗實驗是戴明博士發明用於統計教學的一套工具
這套統計工具可以讓學習者更能體悟到事物變異的情況以及過度調整會發生什麼情形
「過度調整」?
過度調整的英文叫做Over-adjustment
表示系統從原先的狀態被調整而成為另一種不預期的狀態
我們本來的設想是透過某種努力讓系統變得更穩定
然而若我們不具備變異的觀念 以及為何變異會受到系統的干預變得更顯著的話
那我們很有可能會持續犯下錯誤 將共同原因誤判成特殊原因 然後持續犯下錯誤
漏斗實驗富含深意 因為當主管不具備變異知識時 所做出的決策往往擴大變異而非減少變異
當「問題」發生(實際上可能是系統出問題) 我們直覺要「做些什麼」來解決問題
然而漏斗實驗告訴我們 更多時候你什麼都不做還比較好 更重要的是去思考問題的本質
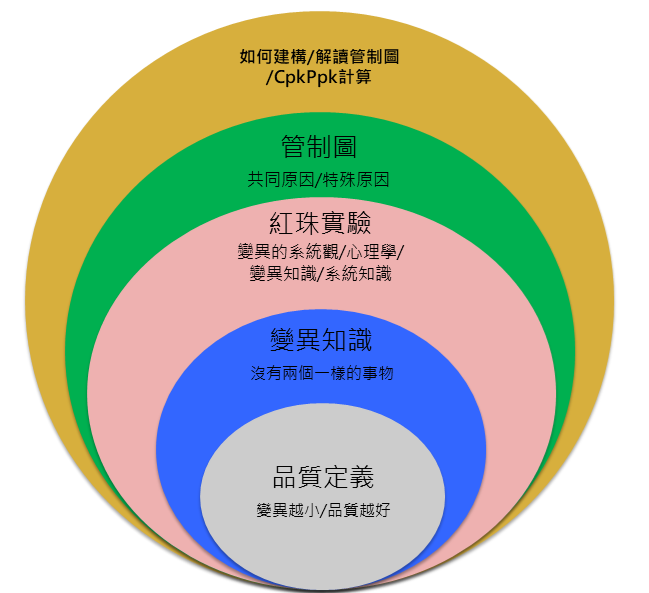
目錄
<情境1>
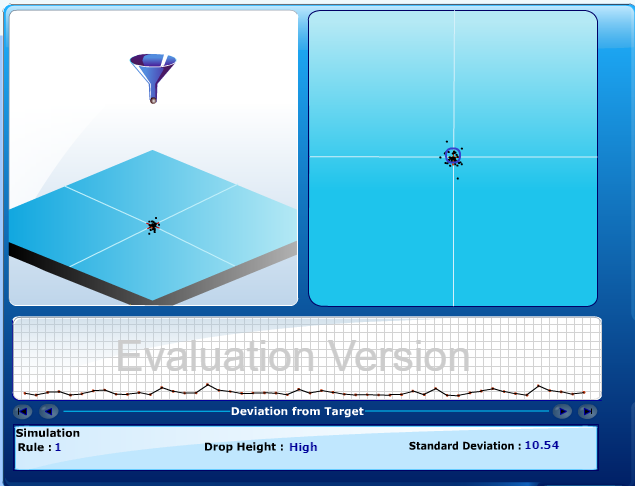
漏斗實驗的初始狀態 讓鋼珠從固定高度的漏斗落下並對準原點 紀錄每一個鋼珠的位置
漏斗的位置沒有改變過 但鋼珠的位置卻出現變異 圍繞著目標散落著
整體的變異不怎麼好 標準差有10.54
情境1就像是我們周遭遇到的「問題」其實已經是穩定的系統
鋼珠從漏斗落下 本來就受到重力及隨機性的影響 進而導致落點位置的變異
這個「問題」是系統的問題 不是任何操作員或者個體能夠操縱的
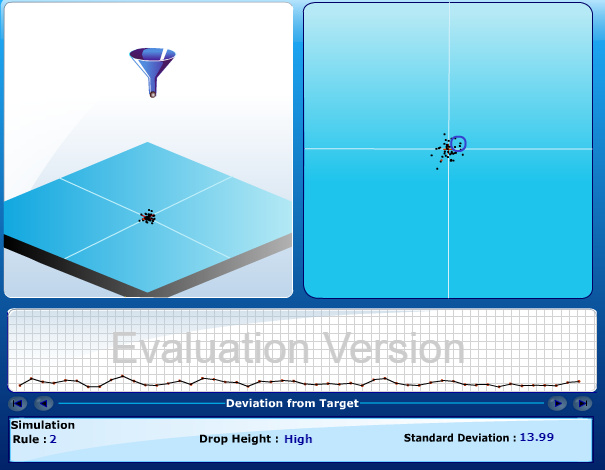
<情境2>
由於情境1的狀況令人不滿 實驗者相信如果可以稍加調整 鋼珠的分布將會變得更集中
所以實驗者根據每一顆鋼珠與原點的距離Z 去調整漏斗的位置
若第一顆鋼珠掉落的距離是5 則漏斗就從上次的位置移動-5的距離用以縮小變異
結果? 結果變異更大 更令人難以接受 這真是令人氣憤!
任何管理者看到這種現象都會破口大罵 是哪個作業員在調整的!
整體的變異不增反減 標準差來到了13.99
情境2則是常見的「矯正措施」
當上一個產品低於規格中心 那我就調升參數讓這一個產品「回歸平均值」
當這一個產品高於規格中心 那我就降低參數讓這一個產品「回歸平均值」
結果越調整越糟糕 而且還沒人搞得懂問題在哪裡?
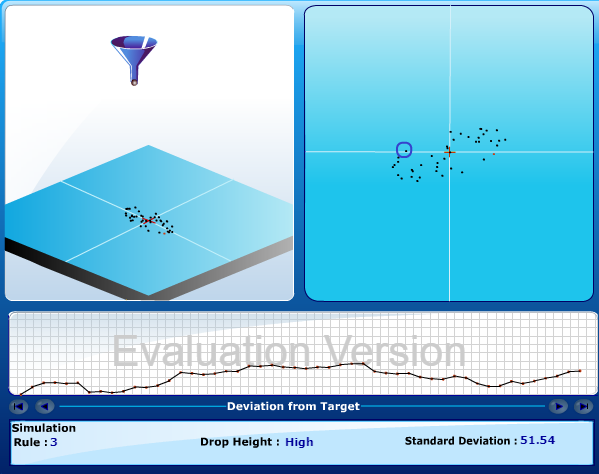
<情境3>
跟情境2的狀況類似 只是情境3是實驗者根據每一顆鋼珠與原點的距離Z去調整漏斗的位置
若第一顆鋼珠掉落的距離是5 則漏斗就從距離原點的位置移動-5的距離用以縮小變異
這樣做沒有比較好 只有更差 管理者到目前為止已經失去耐心!
情境3的狀況與情境2類似 生活上也有類似的例子 例如:賭徒想要翻身 越賭越大
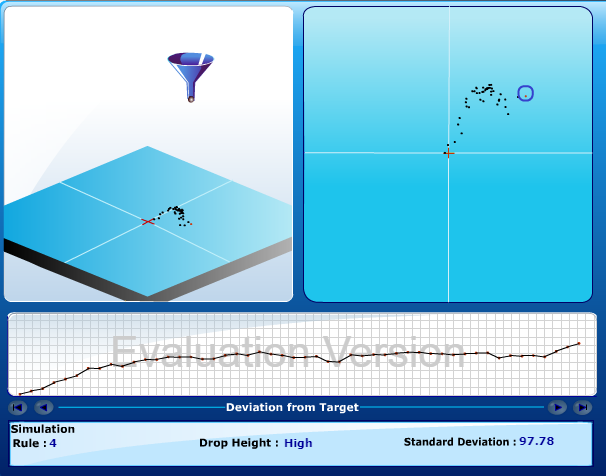
<情境4>
每一次的漏斗位置都放置於上一顆鋼珠掉落的位置上
這樣的變異狀況最慘 變異隨著實驗次數越變越大 跟原來的位置差了十萬八千里
標準差是最爛的 來到97.78
情境4在管理教育訓練很常見 如果教育訓練不是由單一人員教授 而是由人員彼此傳授
那麼每個人都傳授一部分 到最後就會變成四不像 完全失去教育的目的
漏斗實驗想要呈現一件事:若管理者不具備變異的知識 便會在調整的過程犯下錯誤
這項錯誤就是誤將共同原因看做是特殊原因 貿然變更製程參數、製程條件或環境
然後被調整的參數將會使得製程更不穩定 變異越調整越差
那麼怎樣做才能真正從源頭改善漏斗實驗的變異呢?
很簡單 把漏斗的高度降低就可以了 或者你可以選一個比較軟的墊子 讓鋼珠不會滾太遠
你是否具備變異的知識以及識別改善變異是否正確的能力?
延伸閱讀:
https://www.spcforexcel.com/knowledge/variation/overcontrolling-process-funnel-experiment
http://www.symphonytech.com/dfunnel.htm