2023.03.15編修文章
2020.03.26編修文章
Cpk的誤導
許多業界人士以及SPC講師常常會將製程能力指標Cpk掛在嘴邊,彷彿只要Cpk >= 1.33就代表天下太平,製程已經沒有問題了。
然而真的是這樣嗎?Cpk >= 1.33真的表示製程已經穩定且毫無問題嗎? 答案是未必。
這個答案我們從Cpk的計算方式就能一探究竟
Cpk的計算是取min { (USL-Xbarbar)/3(R-bar/d2), (Xbarbar-LSL)/3(R-bar/d2) }
若樣本數據服從常態分配的假設,Cpk的計算方式是去比較「製程中心與規格界限的距離」到底是「製程能力的3倍標準差」的幾倍?
如果這段距離夠大,是製程能力3倍標準差的1.33倍,那我就相信這個製程良好。
但光是樣本數據服從常態分配的假設仍是不足夠的,在某些特殊狀況下,即便數據呈現常態分配且Cpk大於等於1.33仍不表示製程能力良好。這種特殊狀況出現於樣本數據持續上升或下降的時候;此時的數據仍可能服從常態分配,但卻在SPC呈現趨勢性的上升或下降,我們用骰子SPC作為範例,並且使用以下的參數調整
骰子SPC的錯誤示範
1~5 run 骰子點數 = [5,10]
5~15 run 骰子點數 = [3,10]
15~35 run 骰子點數 = [1,10]
35~65 run 骰子點數 = [4,6]
65~85 run 骰子點數 = [3,6]
85~95 run 骰子點數 = [1,6]
95~100 run 骰子點數 = [1,3]
SPC結果如同下圖所示
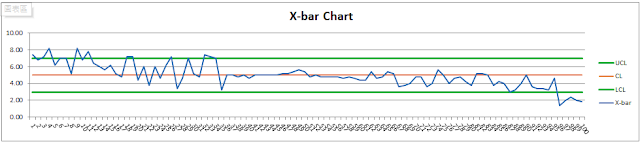
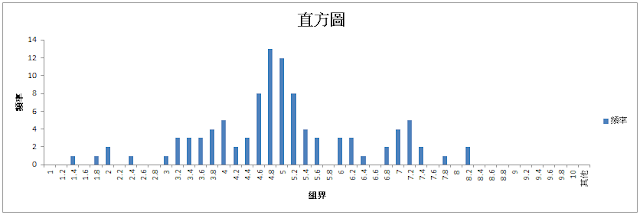
直方圖顯示這個製程很像常態分配,兩側的數據少,中間的數據多;因此如果去計算此製程的Cpk,我們會得到一個不會太差的數據。然而,若我們觀察這個製程的SPC圖型,馬上就可以看到不對勁的地方:數據呈現一種逐漸往下的趨勢,如果你對SPC有概念,大概不會覺得這是個好現象。
改掉錯誤的習慣
回歸到文章開頭提到的問題,好的Cpk就表示製程一定好嗎?
這個問題來自於我在業界常聽到的一句話:「這個SPC的Cpk如何如何」,我們在業界實在太常聽到人們提到Cpk了,然而一再提及Cpk的現象不是一件好事,這點我們已經透過上述的實例證明了,種種事證都說明我們在使用SPC的過程中應該避免單一指標的討論。
下次如果有人提及Cpk >= 1.33就代表此製程已經沒問題了,請記得向他確認其他的製程指標 或者親眼看一下SPC的趨勢性。