上篇文章提到線性最佳解的目標式與限制式
為的是在侷限的限制式範圍中 尋得目標式的極值(最大化或最小化)
為什麼要這麼做呢?理由其實很簡單
因為現實生活中 我們的資源是有限的
如何利用有限的資源 創造最大的價值 就是工業工程在做的事
如同下面的例子(取自維基百科):
假設一個農夫有一塊10平方公尺的地 並種植小麥或大麥或者依某一比例混合種植該農夫只能使用有限的肥料F和農藥P 且小麥的價格為S1 大麥的價格為S2
而單位面積的小麥和大麥都需要不同數量的肥料和農藥
假設X1是小麥的數量 X2是大麥的數量 則問題可以寫成下列形式
max 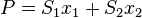 |
(目標函數) | |
| s.t. | 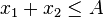 |
(種植面積的限制) |
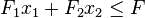 |
(肥料數量的限制) | |
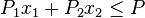 |
(農藥數量的限制) | |
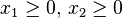 |
(不可以栽種負數的面積) | |
透過以上簡單的數學 我們便得知最有效的種植方式
但還有很多問題沒有解決
種植的過程中或許會遇到小麥跟大麥品質不良的問題
我們想了解小麥與大麥之間是否存在種植品質的差異
這時候統計就派得上用場了
在談統計之前 我們必須先提到機率
機率是什麼呢?機率就是描述事件發生的可能性
事件越可能發生 則機率越大 反之亦然 但最大不超過1 最小不超過0
就像我們丟擲硬幣只會出現兩種結果 不是正面就是反面
正面或反面出現的次數就是我們定義的事件
而硬幣出現正面或反面的可能性 我們定義為機率
這個機率的值 正是你所熟知的1/2
也就是丟擲硬幣有一半的機會出現正面 也有一半的機會出現反面
這個發現實在太重要了
當我們想檢驗這枚硬幣是否公正時 我們就想利用這個發現
A將手中的硬幣丟擲100次 結果出現了38次正面 62次反面
他開始狐疑起來 因為按照一半一半的機率
丟擲100次硬幣會出現接近50次的正面 但卻只有38次
他懷疑這枚硬幣不是公正的硬幣
為了加以證實 他將次數加到1000次 結果得到502次正面 498次反面
這下水落石出了 透過增加丟擲次數(樣本)
硬幣的正反面次數漸漸向1/2靠近 這現象不僅很接近我們的期待
同時更說明了樣本次數與機率分配的因果關係
也就是增加樣本的數量 便可以越靠近真實的機率分配(大數法則)
有了機率與統計的概念
我們應該要了解機率則是描述母體行為的方式
而統計是透過樣本試圖了解母體的過程
如果我們想要知道小麥與大麥之間是否存在種植品質的差異
我們就會取同時間種植的兩者進行比較
比較的基準可能是單位產量 重量等等比較容易量化的指標
然後根據兩者的比較 進一步驗證是否有明顯的差異
(此部分涉及假設檢定 此處不多做說明)
瀏覽次數: -