今年10月在公司內部開了一門課「統計製程分析」英文叫做Statistical Process Analysis
在備課的時候找到了一本原文教科書「Introduction to Statistical Quality Control」
這本書我建議從事品管、品保的人要看 並且推敲裡面講的含義
我簡要摘錄一些作者提到的重點 並且延伸後續我想講的主題
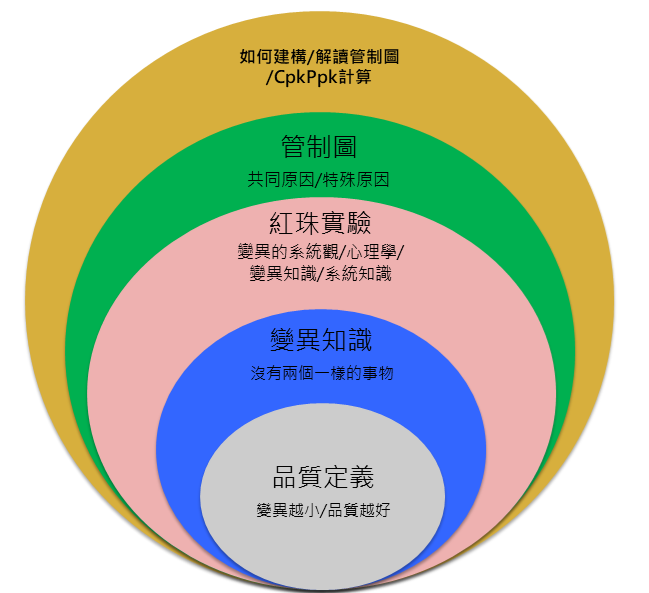
大家都知道品質很重要 但是「品質」這個字彙其實是很抽象的 並沒有實體存在
也因此這樣的抽象詞彙必須要有個定義 並且是大家很容易理解和體認的
才能夠區別品質的好壞、差異 進而處理、改善品質較低劣的部分
在品質管理觀念的發展上不乏品質大師提供的見解與定義
不過我認為沒有一個像下列定義簡潔有力
- 品質是變異的反比 Quality is inversely proportional to variability.
這是互通的道理 你可以從生活、工作上的各種案例發現這些例證
- 品質是預防而非檢驗出來的
「假設檢定的觀念用於辨別某個抽樣的結果究竟屬於兩種不同機制之中的哪一種機制
用句更白話的說法 就是你所觀察到的現象到底是某機制下的偶然 還是另一個機制的常態?
有一個簡單的故事可以說明上述的講法
如果你眼前有一個木箱裝著一個物體 然後秤重出來是315公斤
請問你認為裡面是一頭豬還是裝著一個人?
這題並不是腦筋急轉彎 所以絕大多數的人會猜這木箱裡面裝的是一頭豬
那我們再問 為什麼你會認為這裡面是一頭豬 而不是一個人呢?
多數的人會回答 因為315公斤是一頭豬的機會比較大 人不太可能有315公斤重
當你回答了上述的答案 其實你在心裡已經使用到了假設檢定 並且根據檢定的內容做出判斷
檢定的內容如下
H0 : 木箱內是一個人
H1 : 木箱內不是一個人(是豬)
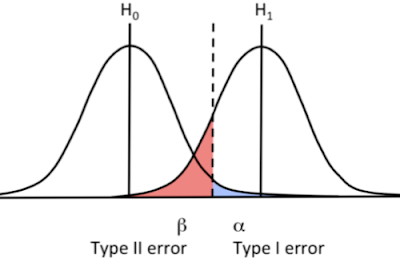
假設檢定實際上就是利用觀察值(也就是虛線部分)去判斷你觀察到的現象屬於哪種機制
並且去計算在H0(null hypothesis)的機制下 比觀察值還要極端的機率是多少
得到的機率我們再跟設定好的alpha(type 1 error, 通常限定為0.05)作比較
如果這個比觀察值更極端的機率比alpha小 那麼我們就傾向於懷疑原始的機制有問題
也就是觀察值很有可能不是出自於你一開始所認知的那個機制(箱子裡面是人)
並且 也是最重要的一點 透過邏輯運算 你很快就會知道結論應該是另外一個機制(箱子裡是豬)
這是因為若P則Q 若非Q則非P的真值表運算 也就是所謂的反證法
沿用人跟豬的範例:
如果箱子裡面是人(P) 則比樣本觀察值還極端的機率不應該那麼小(Q)
但比樣本觀察值還極端的機率非常小(非Q) 所以箱子裡面應該不是人(非P)
這個運算的結果告訴你一件相對可靠但絕非完全正確的結論 也就是木箱內很可能是豬
然而為何是用「可能」而非「一定」是一頭豬呢?
這就牽扯到我們用的抽樣方法了 由於我們用樣本觀察值去觀測母體 所以並不是最完整的資料
這樣的資料存在著必然的誤差(bias) 因此造成了我們推論上的不完美之處
然而如同我們先前提到的 我們已經將這個type 1 error限定在0.05以下 是相對安全的範圍了
講完了假設檢定以及抽樣 我們就挖掘到統計製程管制的核心了
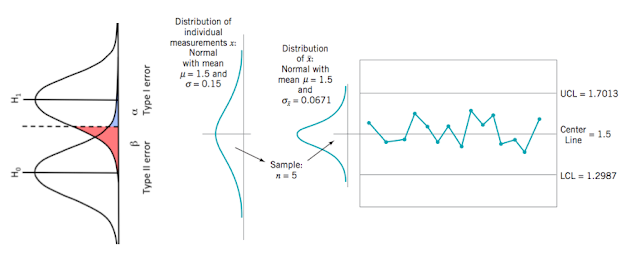
如下圖 我們可以看到SPC的演進就是將分配圖形向左旋轉90度 再逐一描繪樣本平均數的值
並且透過樣本平均數去計算3倍樣本標準差 以得到Control limit UCL & LCL
經過一段時間的累積 出現的圖形就會像最右邊的圖示 是一個由左向右的時間序列
也就是說我們在描繪樣本平均數的值的同時 其實就已經在做假設檢定及統計推論了
這是統計課本上很少提到的觀念 所以在這邊簡單的提一下原理
在取得每一筆樣本觀察值之後 我們其實就會根據它是否落在Control limit之內做出結論
這個結論不外乎:
樣本觀察值落在CL之內 所以相信製程參數還在控制內 or
樣本觀察值落在CL之外 所以相信製程參數已經跑掉了
這不就是假設檢定跟統計推論嗎?是不是覺得所有觀念都是相關且互通的呢?
讀到這裡的各位已經將大學統計課程讀了一遍 也沒有涉及到複雜的數學公式及計算
但你仍然已經熟悉並瞭解了整個統計製程管制的原理、演進以及使用方式
希望對你工作上、統計學分有幫助 有任何問題也歡迎留言討論 謝謝