【品質工程】品質管理的數學工具_貝氏定理Bayesian Theorem

學統計之前要先學機率。

但是當我們提到機率，很多人的腦袋就開始不清楚了，許多人可能想逃避現實，因為機率在學習過程中太痛苦了。

從排列組合開始到條件機率，再到貝氏定理…。條件機率或許還可以撐得下去，但對於機率的定理、公設以及後面推衍的複雜公式已經很少人能招架，然後最近居然有人問我，ㄟ…貝氏定理到底在說什麼呀？

畢業之後我深深體悟到，如果你不能在一分鐘以內表達的概念，那代表你不懂這個概念。這件事也同樣能夠套用在貝氏定理上面，尤其你如果學過但卻又想不起來確切的思路的話。

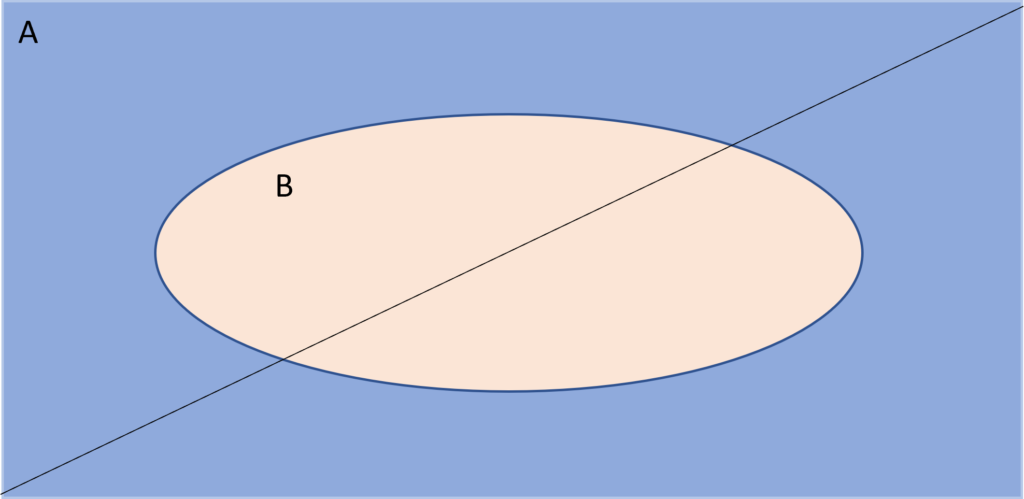
一般來說我們應用條件機率的情境是這樣的：

「在抽菸的前提下，一個人得到肺癌的機率會是多少呢？」如果我們用B代表有抽菸的事件、A代表得到肺癌的事件，我們用機率表達這個問題就變成：P( A | B ) 在B事件發生的情況下A事件發生的機率。這個叫做事後機率，也就是我們在已知B的前提下，想得到A事件的發生機率。

這個先後順序很符合邏輯，因為我們明確了解到是先抽菸才得到肺癌的，在邏輯推論上這就是若P則Q的概念。但是邏輯上只保證若非Q則非P，並不保證若Q則P喔，也就是不保證若有肺癌就是抽菸造成的。

如果將問題換個方向，從已知A事件想得知B事件的機率有多高的話，該怎麼做呢？

同樣的例子，我們想知道「得了肺癌的人是來自於抽菸的比例有多少呢？」這個問題在貝氏定理發展之前是無法回答的。換句話說，原本的問題從順向的問法，變成逆向的問法，時間軸變成先知道結果，再設法取得造成這結果的因子的機率。

貝氏定理很聰明地將原本的條件機率動了一些手腳，轉換成上述提到的問題順序，於是整體的公式就跟原先的條件機率長得很像，卻在思維順序上完全顛倒，這點我想很多老師在教貝氏定理的時候往往都不注重這點，也難怪學生都學得模模糊糊。

貝氏定理的推導過程如下：

由
$P(A｜B) = \frac{P(A \cap B)}{P(B)}$
及
$P(B｜A) = \frac{P(A \cap B)}{P(A)}$
可推得
$P(B｜A) = \frac{P(A｜B)*P(B)}{P(A)}}$

從貝氏定理的推導過程中我們能夠了解一個簡單事實：
當我們想了解在得到肺癌的狀況之下，這情形是抽菸造成的機率有多高？此時這個機率可以透過在肺癌的樣本空間裡面，由抽菸造成肺癌的機率乘以抽菸的機率的比例來得知，上述的文字很繞舌，確實需要一些思考的時間。

有興趣的人可以自行畫出樣本空間分隔圖，這樣可以幫助自己學習。

$P(B_{i}\mid A) = \frac{P(A \mid B_{i})*P(B_{i}}{P(A \mid B_{1})+...+P(A \mid B_{k})*P(B_{k})}$

又因為事件A可以透過全機率分割的概念呈現，所以一般使用時會更常見到上述公式形式。貝氏定理其實是用途相當廣泛的統計工具，在意義上也很容易跟條件機率搞混，我自己本身也花了一些時間重新補完這些細微的觀念，相信會對學習者更有幫助。

貝氏定理在判斷事物的發生機率的時候相當好用，實務上可以幫助我們評估事物發生的機率。

柯文哲市長就曾在”Understanding Human Behaviors from the Perspective of Science”中介紹過貝氏定理的應用，十分精彩，值得一看。

柯市長已經將貝氏定理用十分淺顯的白話文說明了，意思就是「貝氏定理是用來縮小猜測空間的原理」，永遠記得蒐集更多證據來縮減十分難以猜測的可能性，藉以增加做對決策的機會。

在品質管理上也是相同的道理。

如果我們建立了足夠完整的Trouble Shooting Guide，我們也可以應用貝氏定理幫助我們診斷產品目前的失效現象與何種根因有因果關係。這就跟機車行修理機車一樣，有經驗的師傅用耳朵聽哪裡可能有問題；而有將維修經驗寫下來的機車行師傅則會一一蒐集機車的異常現象，藉以更快判斷出問題的根因。

瀏覽次數： -

Recent Posts