【品質工程】品質管理的數學工具_ANOVA變異數分析Analysis of Variance

什麼是ANOVA?

Jeff最近在系統性整理統計學的工具，我們這次先介紹變異數分析。

我會想要寫一篇ANOVA文章的原因很簡單，因為很多人都搞不清楚變異數分析到底在分析什麼東西，即便學過統計的人也有半數以上忘記或根本搞混ANOVA的用途，到後來只會用minitab亂套數據，然後一問三不知。

然而使用ANOVA的情境應該是這樣的：「當我們想了解三個以上的群體的平均表現是否相同時 就會用到這個工具。」

兩群體之間的比較

如果產線有三個相同型號的機台，你如何得知這三台生產的產品表現一樣呢？
如果有人宣稱晶圓的厚度很平均，你怎麼透過觀測該晶圓的四個點做出結論呢？
有補習班老師宣稱他教出來的歷屆學生都會上台大，你怎麼知道每一屆是否都一樣厲害？

這些問題有兩個做法：

你可以每個組合都找10個樣本，然後兩兩比較。這時由於母體變異數未知，你用的是T檢定(關於T檢定還有滿多話題可以聊的)。但是這時候T檢定有個問題，就是兩兩試驗的組數太多了，三個組合的兩兩組合數是C3取2 答案是3組；四個組合的組合數是C4取2，答案是6組，也就是你必須測試3次才能知道這三台的表現到底一不一樣。隨著組數增加，試驗的成本也大幅提升，到最後根本沒辦法執行，因為這樣太沒有效率了，沒人有閒時間搞這些飛機。

如果上述的做法行不通，你也可以用一個golden sample跟每一個組合做比較；但這樣又會讓型一誤差變大(5%變成14.3%，不會算的來找我)，如此一來任何根據這麼大的型一誤差的決策者很容易做錯決策(將好的判定成壞的、把H0的機制判定成H1的機制)。

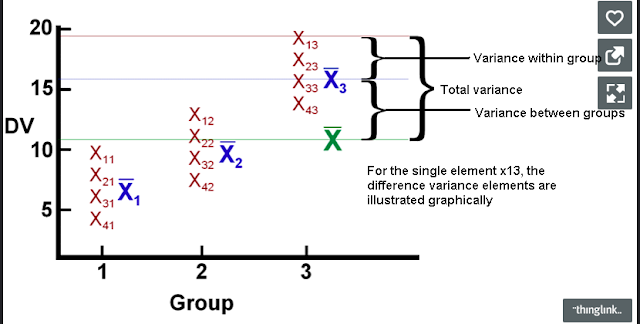
拆解變異
總變異 = 組內變異 + 組間變異
SS_T = SS_W + SS_B

F值的原理

「ANOVA裡面的F值 = 平均組間變異(MST) / 平均組內變異(MSE)就是在陳述上面那段話。

如果我們想要辨別這些群體之間到底有沒有顯著的差異，那麼這些群體的「組間」變異勢必要很大，同時這些群體的「組內」變異要很小，這樣我們才能說群組之間有差異。否則我們就只能相信群體之間沒有差異的假設。」

這就是F分配的由來，也就是兩個變異數相除會形成F分配(關於F分配長什麼樣子再找時間說)。

透過F分配的檢定就能得知數組樣本平均數是否相同的統計推論，於是我們就能透過計算樣本的組間變異、組內變異及總變異，再根據各組變異數數據的自由度取其均方根，讓均方根去平均數據量較多的變異數，得到合理的平均變異(變異數在數據分析上其實代表數據間的「距離」。數據間的距離越遠，則變異越大)。

由於變異數的計算取決於「距離」，所以組內的變異數一定會比組間的變異數來得大，這是因為組內的數據量很多，造成組內的變異總數很大，這時候就需要「平均」這些數據，其中最好的方法就是各自除以各自的「自由度」（至於自由度是什麼 那又是另一段故事了)，再將組間均方根除以組內均方根就能得到F檢定量。

之後就只剩下計算了，公式的部分想學習的人自然能取得公式，只要仔細比對就能了解概念。希望這樣的解釋能讓有興趣投入品質改善的人更懂得變異數分析，也才能更流暢的使用這工具。

變異數分析在統計裡面扮演的角色還不止這樣，它更與迴歸分析、複迴歸分析有關，正確了解、吸收這些數學工具 就能順利學習後面更精深的統計工具(其實也不過就這樣嘛)。

相關文章

【品質工程】品質管理的數學工具_貝氏定理Bayesian Theorem
【品質工程】品質管理的數學工具_假設檢定
【品質工程】品質管理的數學工具_統計分配